부분으로 전체 데이터를 추론할 수 있을까요? 일부 데이터를 가지고 어떻게 전체가 이렇다고 판정할 수 있는 것일까요? 구글 애널리틱스 등의 많은 분석 도구들에서는 샘플링이라는 기법을 사용하여 부분으로 전체를 추론하는데요, 오늘 뷰저블은 이 원리에 대해 설명드리고자 합니다.
매일 기업의 주가는 등락을 반복합니다. 동물병원에 방문하는 개의 신장과 몸무게는 서로 다른 수치로 관측됩니다. 우리는 이처럼 ‘불확실한 현상을 수치화하여 데이터라는 형태로 관측’합니다.
여기서 뷰저블은 여러분들께 한 가지 가정을 제안하려 합니다. 우리에게는 어떤 가방 하나가 있는데 같은 현상을 나타내는 데이터는 모두 이 가방에서 꺼낼 수 있다고 말입니다.
이 가방을 ‘모집단(Population)’이라고 부르겠습니다. 슈퍼마켓의 매출은 슈퍼마켓의 매출이 담긴 가방에서 나오고, 개의 신장(키)는 모두 개의 신장이 담긴 가방에서 나온다고 가정하려 합니다.

여러 분이 좋아하는 연예인 프로듀스 방송에서 후보자에게 투표를 할 때, 모든 데이터는 투표자의 수와 보통 일치하고 유한한 수가 됩니다. 이런 모집단을 우리는 ‘유한 모집단’이라고 부릅니다.
반면 동물병원에 방문한 개의 신장의 경우는 전세계 모든 개들의 길이를 계측해서 그 결과를 무한하게 써놓은 종이들을 가방에 넣었다고 생각해봅시다. 무한개의 데이터가 존재하기 때문에 이 경우를 ‘무한 모집단’이라고 부를 수 있습니다.
오늘 뷰저블 블로그에서는 무한 모집단을 예로 들어 설명하려고 합니다.
모집단(Population)은 연구자가 알고 싶어하는 대상과 집단 전체라고 볼 수 있습니다.
네이버에서 사전을 찾아보면 ‘통계적인 관찰의 대상이 되는 집단 전체’라는 설명이 나오는데요 모집단을 영어로 해석하면 ‘인구’라는 뜻이 됩니다.
왜 모집단을 인구라고 했을까요? 왜냐하면 모집단은 ‘전체 집단’을 나타내기 때문입니다. 어느 분석가가 대한민국 남성의 평균 키를 알고 싶다고 한다면, 모집단은 대한민국 남성이 되고, 21대 국회의원 선거 결과가 알고 싶다면 마찬가지로 모집단은 대한민국 전체 국민의 투표 내용이 될 것입니다.
추상적인 개념이라 이해하기 어렵겠지만, 분석가가 알고자 하는 ‘전체 집단’ 그 자체라고 해석해봅시다. 위에서도 말한것처럼 ‘가방’이고 데이터를 이 가방에서만 꺼낸다고 생각하면 개념이 한걸음 더 쉬워질 것입니다!
김치찌개 한 숟가락만 맛 보고서 전체 냄비에 담긴 찌개의 간이
딱 맞을 거라고 판정하는 예시가 샘플링의 기본적인 원리에 해당합니다.
어떻게 부분 데이터를 가지고 전체 데이터를 추론할 수 있을까요? 우리 일상생활 속을 자세히 들여다보면 흔히 일어나는 일입니다.
보글 보글 맛있는 김치찌개를 끓인 여러분은 찌개의 간이 맞는지를 보기 위해 한 수저 떠먹어 보곤 그 한 수저가 맛있다면 냄비 속 전체 김치찌개의 간도 맞을 거라고 판단하지 않으신가요? 굳이 냄비 속 모든 김치찌개를 다 먹어보지 않고 딱 한수저로 판단을 해버리죠. 이것이 바로 부분으로 전체를 판정하는 대표적인 예시입니다!
다만 찌개를 맛볼 때 우연히 진하게 우러나온 부분을 떠먹어볼 수도 있을 것입니다. 그렇기 떄문에 전체의 맛은 한 수저 맛을 볼 때와 ‘조금은 다를 가능성’이 존재함을 고려해야 합니다.
통계적 추정은 100% 일치한다고 볼 수 없으며 얼마만큼은 오차가 존재할 것이라고 생각할 수 있습니다.
모집단과 랜덤 샘플링의 개념을 풀장의 공으로 알아보기
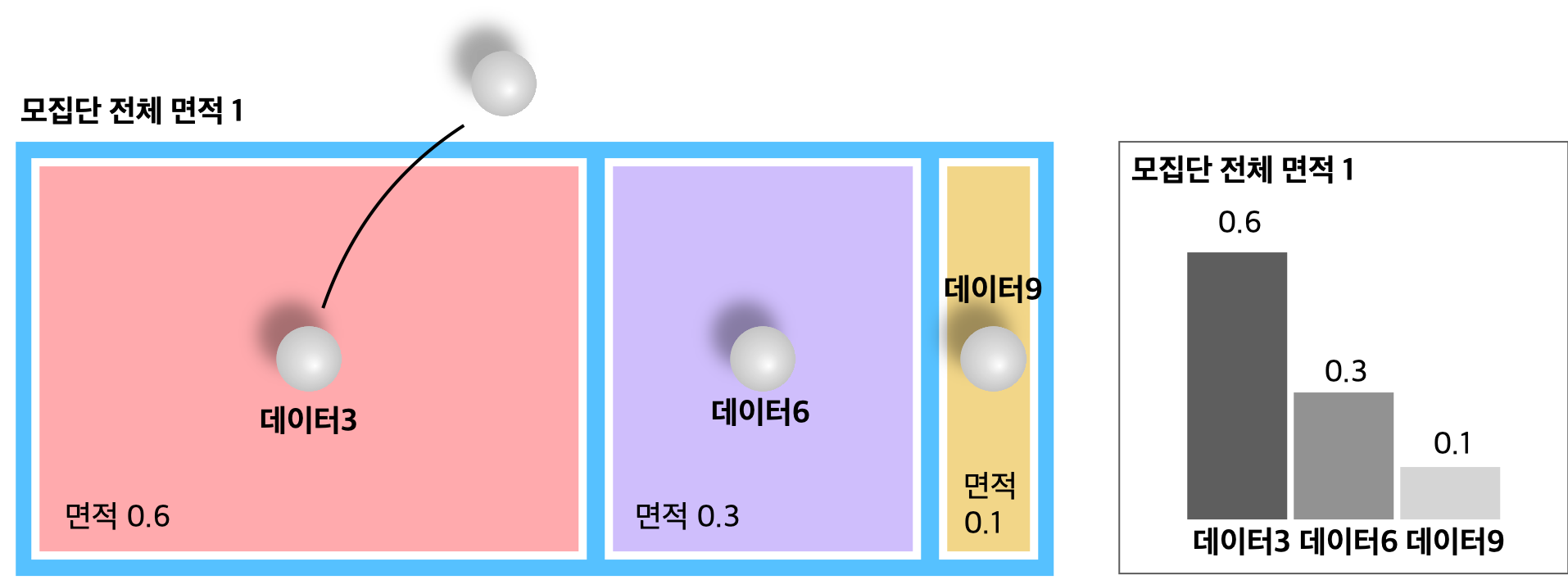
무한 모집단의 구조를 위 이미지와 함께 공과 풀장에 빗대어 설명하겠습니다.
- 무수한 숫자 공들이 풀장 안에 있는데, 같은 숫자 공은 동일 색상 풀 위에 있습니다.
- 풀장 면적은 차이가 있으나 전체 합이 1인 소수로 이뤄집니다.
- 어떤 풀장에서 공을 하나씩 꺼내 데이터(표본)로 꺼냅니다.
- 어떤 풀장에서 나오는가는 풀장의 면적에 비례합니다.
각각 다른 색으로 표기된 풀장에는 ‘데이터 3’, ‘데이터 6’, ‘데이터 9’라는 종류의 공들이 들어있고 무수히 존재합니다. 분홍색 풀장은 ‘데이터 3’이 무수히 많이 들어 있는 풀장, 보라색 풀장은 ‘데이터 6’, 노란색 풀장에는 ‘데이터 9’가 무수히 많이 들어있다고 가정합시다.
풀장은 넓이가 달라서 각각 0.6, 0.3, 0.1의 면적을 갖고 있는데 모두 합하면 1이 됩니다. 풀장의 넓이는 모집단이라는 풀장 속 데이터 공들이 ‘얼마나 쉽게 튀어 나오는가’로 해석할 수 있습니다.
이 풀장에서 관측되는 데이터는 3과 6, 9 셋 중 하나겠지만 빈도는 넓이에 따라 달라질 것입니다. 관측되는 숫자 3은 숫자 9의 6배가 되는 것처럼 말입니다.
위 풀장(모집단)에서 충분할 정도로 반복해서 데이터를 관측해보면 해당 히스토그램은 거의 모집단과 일치하게 됩니다. 이러한 가정을 기본적인 샘플링이라 볼 수 있는 랜덤 샘플링의 가정, 즉 ‘무작위 추출의 가정’이라고 볼 수 있습니다.
오늘 블로그에서 배운 내용들을 기반으로 샘플링의 기본 원리를 정리하면, 충분한 횟수로 공들의 숫자를 관측하고, 관측된 데이터의 분포가 모집단의 분포 모습과 상당히 정확하게 재현된다는 사실을 밝혀내야 한다고 이해할 수 있습니다. 하지만 실제로 이렇게 조사하는 것은 거의 불가능하기 때문에 많이 관측되지 않은 데이터로부터 모평균을 추측하는 방법을 활용해야 합니다.
이번 글에서는 기초 개념을 설명하기 위해 생략하고 다음 기회에 재차 알려드리겠습니다.
샘플링의 장단점과 편향될 수 있는 주요 이유 알아보기
샘플링의 장점으로는 모집단 전체를 분석하지 않아도 되기 때문에 데이터 규모가 상당히 크나 특정 수치를 연산하는 데에 서버 등의 인프라가 갖춰져 있지 않을 경우 굉장히 분석이 용이합니다.
반면 모집단의 크기가 작을 경우에는 샘플링이 의미가 없어지고 샘플이 모집단을 잘 대표해야만 일반화가 가능합니다.
샘플링이 편향될 수 있는 이유로는 주로 아래 4가지가 있습니다.
- Quota Sampling Bias : 샘플을 잘못 할당하는 것에서 생길 수 있는 편향성입니다.
- Selection Bias : 특정 집단을 집중적으로 선택하는 것에서 생길 수 있는 편향성입니다.
- Size Bias : 특정 집단에게 표본으로 선정될 수 있는 특혜를 줌으로써 생길 수 있는 편향성입니다.
- Under Coverage Bias : 특정 집단을 누락시키는 것에서 생길 수 있는 편향성입니다.
편향되지 않은 샘플이란 것이 존재할 수 있을까요?
한 수저 떠먹어 본 김치찌개가 우연히 진하게 우러나온 부분일 수 있다고 위 글에서 언급한 것처럼, 결론적으로 편향되지 않은 샘플이란 있을 수 없습니다. 완벽하게 모집단을 대표할 수 있는 샘플이란 존재하지 않는 것이죠. 최대한 편향적을 억제하기 위해 노력한다고 보는 것이 좋을 것 같습니다.
참고할 수 있는 자료: 샘플을 편향되게 만들 수 있는 9가지 방법
뷰저블도 샘플링된 데이터를 제공하나요?
뷰저블에서는 샘플링된 데이터를 제공하지 않습니다.
고객을 위한 비용 외의 모든 낭비를 제거하고 최소화하여, 우리가 가장 중요한 가치로 여기는 ‘정확도 높은 데이터’를 제공하기 위해 노력합니다. 샘플링은 위에서도 언급한것처럼 데이터 연산의 부담을 줄여줄 수 있지만 위에서 말한 편향들을 억제할 순 없기 때문입니다.
구글 애널리틱스 등의 다양한 서비스에서는 이러한 샘플링을, 전체 데이터를 보기 위해서는 유료 서비스로 전환하라고 제시하는 ‘비즈니스 전략’으로 활용하기도 하지만 뷰저블에서는 현재 전체 데이터를 제공하는 것을 원칙으로 하고 있습니다.
완벽한 데이터란 있을 수 없습니다.
우리에게 중요한 것은 데이터 속에서 귀중한 인사이트를 발견하고 조직이 실행할만한 방안을 찾을 수 있는가란 사실을 놓치지 마세요!







